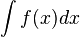En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
La factorización de enteros en números primos se describe en el teorema fundamental de la aritmética y la factorización de polinomios (en ciertos contextos) en el teorema fundamental del álgebra.
BINOMIOS CONJUGADOS:
En álgebra, un binomio es una expresión algebraica con dos términos. Estrictamente hablando se refiere a un polinomio formado por la suma de dos monomios
Al efectuar productos con binomios que tienen los mismos términos podemos obtener lo siguiente: (a+b)²= (a+b)(a+b)
Bajo la definición estricta, son binomios las expresiones:
mientras que no lo son expresiones tales como:
puesto que alguno de sus términos no es un monomio, aunque en un contexto más informal podría llamarse binomio a cualquier expresión que involucre una suma o resta de dos expresiones. Así, es posible encontrar en un libro de álgebra un ejercicio en la sección de "binomios al cuadrado" que diga «Calcula el resultado de (cos(x)+sen(x))2».
Grado de un binomio
Para hallar el grado de un binomio :Éste se calcula sumando los exponentes de cada término algebraico. La mayor suma es el grado. (x+y)(x+y)= (x+y)2= x2 + 2x2y + y2- Así, en el binomio
 el primer monomio tiene grado 2+5+2+1 = 10, mientras que el grado del segundo es 3+9+2 = 14, por lo que el binomio tiene grado 14.
el primer monomio tiene grado 2+5+2+1 = 10, mientras que el grado del segundo es 3+9+2 = 14, por lo que el binomio tiene grado 14.
Productos notables
Existen ciertas fórmulas que permiten multiplicar ciertos polinomios de forma directa (sin realizar la multiplicación completa). Tales fórmulas se denominan productos notables y muchas de ellas se refieren a operaciones con binomios. Estos productos suelen ser estudiados con detalle en los primeros cursos de álgebra.TRINOMIOS CUADRATICOS:
TRINOMIOS CUADRADOS PERFECTOS | |
Esta es la factorizacion del primer tipo de trinomio cuadrado perfecto, en el cual todos los terminos son positivos:
|
 | |
Este es el segundo tipo de trinomio cuadrado perfecto, se diferencia del anterior en que el segundo termino, es negativo:
|
TRINOMIOS CUADRATICOS | |
Esta es la factorizacion de un trinomio cuadratico del tipo mas elemental. La regla para factorizar este tipo de expresiones consiste en lo siguiente:
|
TRINOMIOS CUADRATICOS GENERALES | |
Esta es la factorizacion de un trinomio cuadratico general. El procedimiento mas facil es por ensayo y error y se realiza de la siguiente manera:
INTEGRACION POR CAMBIO DE VARIABLES: El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta. Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla. Pasos para integrar por cambio de variable1º Se hace el cambio de variable y se diferencia en los dos términos: Se despeja u y dx, sutituyendo en la integral:  2º Si la integral resultante es más sencilla, integramos: 3º Se vuelve a la variable inical: Ejemplo      Cambios de variables usuales1. 2. 3. 4.  5. En las funciones racionales de radicales con distintos índices, de un mismo radicando lineal ax + b, el cambio de variable es t elevado al mínimo común múltiplo de los índices. 6. Si  7. Si  |





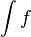 ó
ó